ترجمه‌های کامران بزرگزاد
توجه: به دلیل کامل نبودن این فایل، ممکن است برخی از لینک‌های کار
نکنند.
این کتاب مرور کوتاهی دارد بر مهمترین
موضوعاتِ ریاضی و سیر تحول این علم را از هزاره اول پیش از میلاد تا اواخر قرن
بیستم بررسی می‌کند. کتاب جنبه تاریخی اندکی دارد، در عوض کاری که انجام می‌دهد
این است که مهمترین ابداعات و موضوعاتی که در این علم پدید آمده، و کلاً آنچه
ریاضیات معاصر بر پایه آنها شکل گرفته، را مرور می‌کند.
کسی که دانش آموخته ریاضی است، و حداقل
مدرک کارشناسی این رشته را دارد، چیزی حدود 6000 صفحه کتاب ریاضی خوانده، که حدود
2000 صفحه آن به دوره ابتدایی و متوسطه مربوط است و شامل کتاب‌های مختلف درسی مثل
حساب، هندسه، جبر، حسابان، و غیره می‌شود
که دانش‌آموزان در طول 12 سال یاد می‌گیرند، و حدود 4000 صفحه دیگر هم به کتاب‌های
تخصصی مربوط است که در دانشگاه می‌خوانند (حسابان پیشرفته، معادلات دیفرانسیل، جبر
خطی، جبر مجرد، آنالیز مختلط، ...). کسی که ریاضی خوانده، حتماً باید همین حجم از
دانش ریاضی را یادگرفته باشد، اگر او نابغه باشد، ممکن است همه این 6000 صفحه را
بجای 16 سال، در طول سالیان کمتری یاد بگیرد، ولی حجم کلی کتابهایی که باید برای
کسب مدرک کارشناسی ریاضی خوانده شود، کم و بیش همین قدر است.
بنابراین،
همانطور که نویسنده در مقدمه خود اشاره می‌کند، فقط یک
فرد ناآگاه می‌تواند تصور کند که کُل ریاضیات را بتوان در 200 بخش کوچک خلاصه کرد.
پس از این کتاب نمی‌توان انتظار آموزشِ مطالبی را داشت که در بخش‌های مختلف به شکل
فهرست‌وار به آنها اشاره شده، زیرا با حجم اندکی که دارد، فقط می‌تواند سرفصل‌ها
و تحولات عمده را مرور کند، که البته اینکار با ذکر برخی از جزئیات فنی
انجام شده است.
این کتاب
حاوی حدود 200 بخش است که موضوعات مهم و دگرگون کننده مطرح در ریاضیات را مرور می‌کند.
این بخش‌ها خیلی کوتاه هستند و هر یک از آنها را می‌توان در یکی دو دقیقه مطالعه
کرد. در نتیجه مطالعه این کتاب، و مرور ریاضیات، بر حسب سرعت خواننده، حدود 4 ساعت
طول خواهد کشید.
این کتاب
می‌تواند برای کسانی که قبلاً ریاضیات خوانده‌اند، یا مشغول یادگیری آن هستند جالب
باشد. کسانی که ریاضیات می‌خوانند، یا در کل به این دانش علاقمندند، مطالبی را در
این کتاب می‌بینند که ممکن است برای آنها مفید باشد. دانش‌آموز دبیرستان می‌توانند
6 فصل اول کتاب را به راحتی بخوانند و با آن احساس آشنایی کنند، و حتی اگر فصول
بعدی برای آنها نامانوس و گنگ باشد، آنها می‌توانند با موضوعات ریاضی که بعداً در
دانشگاه با آن روبرو خواهند شد بهتر آشنا شوند. اگر هم آنها جزء کسانی باشند که
خیلی با ریاضیات سر و کار دارند، مثلِ دانشجویان رشته ریاضی، یا دانشجویان فنی و
مهندسی، می‌توانند بر آنچه قبلاً یادگرفته‌اند مروری داشته باشند، ارتباط آنها را
منسجم‌تر درک کنند، یا شاید هم اگر جزء دانشجویان قدیمی سی/چهل سال قبل باشند،
موضوعاتی را پیدا کنند که برای آنها تازگی داشته باشد.
پال گلندِنینگ (Paul Glendinning) متولد 1958، ریاضیدان انگلیسی است. او در سال 1986 دکترای خودش را از
دانشگاه کینگز کالج کمبریج دریافت کرد، و حالا استاد برجسته دانشگاه منچستر در
رشته ریاضیات کاربردی است.
گلندِنینگ در خیلی از دانشگاه‌های معتبر انگلستان تدریس کرده. تخصص او در
سیستم‌های دینامیکی است و تا کنون بیش از 15 کتاب درسی و 30 مقاله از او منتشر
شده.
پاییز 1403
کامران بزرگزاد
ایمانی
ریاضیات بیش از چهار هزار سال است که در
حال تکامل می‌باشد. ما هنوز هم زوایا را با استفاده از سیستم 360 درجه‌ای، که توسط
بابلیان باستان ابداع شده بود، اندازه‌گیری می‌کنیم. هندسه در یونانیان باستان
متولد شد. یونانیان همچنین برای نخستین بار به وجود اعداد گنگ پی بردند. تمدن‌های
اسلامی جبر را توسعه دادند و استفاده از صفر را به عنوان یک عدد رواج دادند.
بنابر یک دلیل موجه، ریاضیات یک سابقه
غنی دارد. دلیلش هم این است که این علم به طرز خیره‌کننده‌ای مفید است، زیرا نه
تنها زبان علم، فناوری، معماری، و تجارت است، بلکه به‌عنوان یک فعالیتِ فکری می‌تواند
بسیار رضایت‌بخش باشد. ریاضیات نه تنها یک سابقه غنی دارد، بلکه همچنان به تکامل
خود ادامه می‌دهد، هم در کاربرد روش‌های خودش در حوزه‌های تثبیت شده علم، و هم در
کشف یا اختراع حوزه‌های جدیدِ تحقیق. اخیراً کامپیوتر‌ها راه‌های جدیدی برای کشف
ناشناخته‌ها ارائه کرده‌اند، و حتی اگر هدف نهایی ریاضیدانان ارائه اثبات‌های
سنتی باشند، شبیه‌سازی‌های عددی می‌توانند منابع شهودی جدیدی را برای ریاضیدانان
فراهم کنند که روند شکل‌دهی حدس‌ها، و نهایتاً اثبات‌های آنها را سرعت بخشد.
تنها یک انسان ناآگاه
می‌تواند وانمود کند که کُل ریاضیات را می‌توان در 200 بخش کوچک معرفی کرد. آنچه
این کتاب سعی در انجام آن دارد این است که برخی از دستاوردهای قدیمی و جدید
ریاضیات را شرح دهد و توضیح دهد که چرا این موضوعات بسیار هیجان انگیز هستند. به
منظور بسط برخی از ایده‌ها با جزئیات بیشتر، طبیعی به نظر می‌رسید که بر هسته
ریاضی آنها تمرکز کنیم. ما کاربردهای وسیع این ایده‌ها را فقط به صورت گذرا ذکر
کرده‌ایم.
ایده‌های ریاضی بر روی یکدیگر بنا می‌شوند،
بنابراین به طور منطقی موضوعات این کتاب به‌گونه‌ای سازماندهی شده‌اند که حوزه‌هایی
که ریشه مشترکی دارند، در فصول نزدیک به هم مطرح شوند. اما خواننده باید به
پیوندهای ناپیدای این موضوعات توجه داشته باشد. یکی از ویژگیهای شگفت‌انگیز
ریاضیات این است که حوزه‌هایی که ظاهراً جدا از هم به نظر می‌رسند، عمیقاً به هم
مرتبط هستند. حدس‌های هیولاگونه مون‌شاین (به
این قسمت رجوع کنید) نمونه جدیدی از این موضوع را ارائه می‌دهد و معادلات
ماتریسی پیوند محکم‌تری را میان حوزه‌های مختلف ارائه می‌دهد.
بنابراین این کتاب چکیده کوچکی از چهار
هزار سال تلاش بشر است، اما تنها می‌تواند یک آغاز باشد، آغازی که امیدوارم مبداء
مطالعات بیشتر و تفکرات عمیق‌تر برای خواننده باشد.
پال گلندِنینگ
در ساده‌ترین تعریف، اعداد فقط صفاتی هستند
که کمیت‌ها را توصیف می‌کنند. مثلاً شما ممکن است بگوییم «سه تا صندلی» یا «دو تا
گوسفند». اما حتی اگر عدد را به عنوان یک صفت در نظر بگیریم، ما به طور غریزی درک
می‌کنیم که عبارتی مثل "دو تا و نصفی بُز" معنایی ندارد. بنابراین،
اعداد می‌توانند کاربردها و معانی متفاوتی داشته باشند.
در طول دورانی که مردمان باستان از
اعداد به روش‌های مختلف استفاده می‌کردند، این اعداد معانی نمادین پیدا کردند.
مثلاً نیلوفر آبی در هیروگلیف‌های مصری عدد 1000 را نشان می‌دهد. اگرچه این تصاویر
از نظر زیبایی شناختی دلپذیر هستند، اما در عملیات جبری نمی‌توان از آنها استفاده
کرد. همانطور که کاربرد اعداد بیشتر شد، علائم نشان دهنده آنها نیز ساده‌تر شدند.
رومی‌ها از گروه کوچکی از حروف اصلی برای نشان دادن تعداد وسیعی از اعداد استفاده
می‌کردند. ولی محاسبات روی اعداد بزرگ به روش آنها پیچیده بود.
دستگاه عدد نویسی نوین (به اینجا مراجعه کنید) از تمدن‌های عربی
هزاره اول به ما به ارث رسیده است. این دستگاه که از عدد 10 به عنوان پایه استفاده
می‌کند، عملیاتِ پیچیده را بسیار آسان‌تر می‌کند.
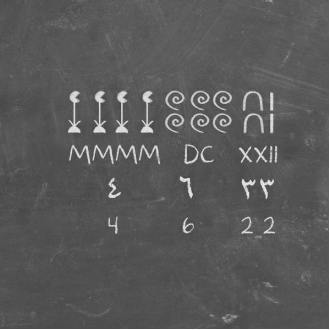
عدد نویسی‌های مختلف: (ردیف بالا) هیروگریف مصری. (ردیف دوم) عدد نویسی
رومی. (ردیف سوم و چهارم) عدد نویسی هندی-عربی.
اعداد طبیعی اعداد شمارشی ساده هستند (0, 1, 2, 3, 4, . . .) . مهارت در شمارش ارتباط
نزدیکی با توسعه جوامع پیچیده از طریق تجارت، فناوری، و گردآوری اسناد دارد. با
این حال، شمارش به چیز بیشری از اعداد نیاز دارد. این شامل عملیاتی نظیر جمع، و
عکس آن تفریق، نیز می‌شود.
به محض اینکه پای شمارش به میان آمد،
عملیات عددی نیز بخشی از ماجرا می‌شوند. در این مرحله، اعداد فقط یک صفت ساده
نیستند و به اشیایی تبدیل می‌شوند که می‌توانند با هم ترکیب شوند. هنگامی‌که
مفهومِ جمع معلوم شد، ضرب نیز به عنوان روشی برای محاسبه مجموعِ جمع‌ها در نظر
گرفته می‌شود، مثلاً می‌توان پرسید در پنج گروه شش‌تایی از اشیاء، کلاً چند شیء
وجود دارد؟ در همین حال، تقسیم راهی برای توصیف عملِ مخالفِ ضرب ارائه می‌دهد،
مثلاً می‌توان پرسید، اگر 30 شئ به پنج گروه مساوی تقسیم شوند، در هر گروه چند شئ
وجود دارد؟
اما مشکلاتی نیز پیش خواهد آمد. مثلاً،
منظور ما از تقسیم 31 شئ به 5 گروه مساوی چیست؟ 1 را بر 10 تقسیم کردن یعنی چه؟
برای درک این سؤالات باید از اعداد طبیعی فراتر برویم.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
به طور ساده می‌توانیم بگوییم که یک
مجموعه دسته‌ای از اشیاء است.
اشیاء درون یک مجموعه به عنوان اعضاء یا عناصر (elements) آن شناخته می‌شوند. ایده مجموعه، ایده‌ای بسیار قوی است، و مجموعه‌ها از
بسیاری جهات بلوک‌های سازنده و بنیادی ریاضیات را
تشکیل می‌دهند که حتی از اعداد نیز بنیادی‌تر هستند.
تعداد عضوهای یک مجموعه می‌تواند محدود
و متناهی، یا نامتناهی باشد. معمولاً این عضوها با قرار دادن آنها در آکولاد { }
نمایش داده می‌شود. ترتیب نوشته شدن عضوها در مجموعه‌ها، و همینطور تکرار یک عضو
در آنها، اهمیتی ندارد. همچنین ممکن است یک مجموعه از مجموعه‌های دیگری ساخته شده
باشد، هرچند باید در توصیف آنها دقت زیادی کرد.
یکی از دلایل مفید بودن مجموعه‌ها این
است که به ما اجازه می‌دهند کلیت را حفظ کنیم، و تا حد امکان، به اشیاء مورد
مطالعه ساختار کمتری را نسبت دهیم. عضوهای درون یک مجموعه می‌توانند هر چیزی
باشند، از اعداد گرفته تا اشخاص، یا
سیارات، یا ترکیبی از هر سه ، هرچند در کاربردهای مختلف، معمولاً عضوهای درون یک
مجموعه به طریقی به هم مرتبط هستند.
هر دو مجموعه مفروضی که داشته باشیم، می‌توانیم عملیات
مختلفی را روی آنها بکار گرفته و مجموعه‌های جدیدی را ایجاد کنیم. برخی از این
عملیات علائم مخصوص به خودشان را دارند.
اشتراک (intersection) دو مجموعه X و Y، که آن را به صورت X∩Y می‌نویسیم،
مجموعه همه عضوهایی است که هم عضوی از X و هم عضوی از Y باشند،
ولی اجتماع (union) دو مجموعه X و Y، که آن را به صورت X∪Y نمایش می‌دهیم، مجموعه همه
عضوهایی است که در دو مجموعه X و Y
هستند.
مجموعه تهی
(empty set)، که به صورت {} یا ∅ نشان داده می‌شود،
مجموعه‌ای است که کلاً هیچ عضوی ندارد. یک زیرمجموعه از مجموعه X مجموعه‌ای
است که همه عضوهای آن در X قرار دارند، که ممکن است شامل برخی یا همه عناصر X باشد.
مجموعه تهی می‌تواند زیرمجموعه تمام مجموعه‌ها باشد.
مجموعه متمم (complement) Y، که بصورت 
نوشته می‌شود، مجموعه‌ای از عضوها است که عضوی از Y نیستند.
اگر Y زیرمجموعه‌ای از X باشد، متمم نسبی Y که بصورت X\Y
نوشته می‌شود، مجموعه عضوهایی در X هستند که در Y
نیستند، و غالباً از آن به عنوان X not Y اشاره می‌شود.
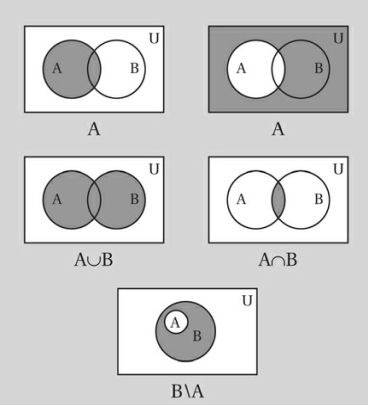
چند نمودار ساده وِن برای برخی عملیات اصلی مجموعه‌ها.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
دنباله‌های ریاضی فهرست‌های منظمی‌از
اعداد هستند. مانند مجموعه‌ها (به اینجا مراجعه
کنید)، دنباله‌ها می‌توانند بی‌پایان، یا بی‌نهایت باشند. برخلاف مجموعه‌ها،
عضوها یا جملات درون یک دنباله دارای ترتیب خاصی هستند و یک جمله می‌توانند در
نقاط مختلف فهرست تکرار شود.
فهرست اعداد طبیعی، یعنی 1،
2، 3، .
. . ، معروف‌ترین
دنباله است. فاصله جملات این دنباله از هم
مساوی هستند و تا بی‌نهایت ادامه دارند. در انواع دیگری از دنباله‌ها، مثلاً دنباله
فیبوناچی، فاصله بین جملات هربار بزرگتر می‌شود. دنباله‌های مذکور با هم
متفاوتند. دنباله‌های دیگری نیز هستند که همگرا (convergent) نامیده می‌شوند و وقتی تعداد جملات آنها به بی‌نهایت می‌رسد، به مقدار
خاصی نزدیک می‌شوند.
در یک دنباله نشان دهنده واپاشی رادیواکتیو، که
در آن مقدار باقیمانده یک ایزوتوپ رادیواکتیو در یک بازه منظم به نام "نیمه
عمر" به نصف می‌رسد، جملات موجود با پیشرفت دنباله به صفر نزدیک می‌شوند. همانطور که در زیر نشان داده شده، این دنباله
همگرا را می‌توان با یک منحنی فروپاشی نمایی نشان داد.
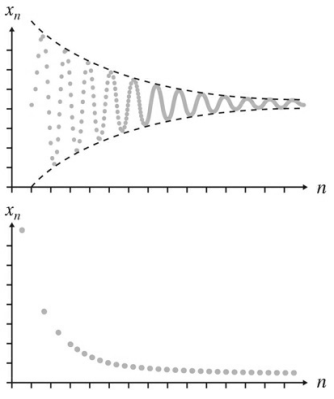
نمونه‌هایی از یک دنباله همگرا (بالا)،
و یک دنباله واپاشی نمایی، مانند نیمه عمر رادیواکتیو (پایین).
یک سری ریاضی، عبارتی برای مجموعِ جملات
درون یک دنباله است. یک سری که معمولاً با حرف یونانی ∑ (سیگما) نشان داده می‌شود،
می‌تواند مجموعِ تعداد نامتناهی از جملات، یا بُرد محدودی از جملات باشد. در هر
صورت، حد پایینی و بالایی محدوده در پایین و بالای علامت ∑ نوشته می‌شود.
هر دنباله مفروضی از اعداد، که جملات آن
بصورت an
نوشته می‌شود، سری آن بصورت یک مجموع نامتناهی است:
در بسیاری از موارد، این مجموع به بی
نهایت میل می‌کند، یا ممکن است به مقدار خاصی نزدیک نشود. ولی سری‌هایی وجود دارند که در آنها این مجموع
به سمت یک مقدار خاص، که حد (limit) نامیده می‌شود، میل می‌کنند.
برای اینکه ببینیم آیا یک سری حد معینی دارد یا خیر، مجموع جزئی محدود Sn را به عنوان مجموع اولین n+1 جمله،یعنی a0+a1+. . .+an تعریف می‌کنیم. اگر برای هر
مقدار از n، دنباله جزئی مجموع‌ها به سمت L
میل کند، این دنباله به حد L همگرا خواهد شد.
...........................................
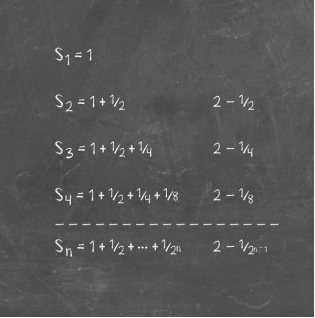
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه این کتاب می‌توانید
نسخه کامل PDF آن
را تهیه کنید.
هندسه عبارت است از مطالعه اشکال، یعنی
اندازه آنها، موقعیت آنها، و فضایی که این اشکال در آن قرار می‌گیرند. این شاخه به
شکل کلاسیک، در حدود 300 سال قبل از میلاد توسط ریاضیدان یونانی اقلیدس (Euclid) بر اساس فهرستی از اشیاء و فرضیاتی که اصول موضوعه نامیده می‌شوند
و همه نتایج از آن پیروی می‌کنند، بنا نهاده شد.
کتاب
بسیار مهم اقلیدس، به نام اصول (Elements)،
پنج اصل موضوعه زیر را ذکر می‌کند:
1.
از میان هر دو
نقطه می‌توان خطی را رسم کرد.
2.
یک پاره خط را
می‌توان از هر جهت تا بی‌نهایت امتداد داد.
3.
به مرکز هر
نقطه می‌توان یک دایره با هر شعاعی رسم کرد.
4.
هر دو زاویه
قائمه با هم برابرند.
5. برای یک خط مستقیمِ مفروض، و نقطه‌ای که خارج این خط
است، دقیقاً یک خط از نقطه عبور می‌کند که خط اصلی را قطع نمی‌کند، و با خط اصلی
موازی است.
شایان ذکر است که اصول موضوعه اقلیدس از
تعدادی اصطلاح، مانند خط، زاویه قائمه، و شعاع استفاده می‌کند بدون اینکه توضیحی
برای آنها ارائه دهد یا آنها را تعریف کند. در نتیجه در اواخر دهه 1800، بر اساس
چارچوبی کاملاً منطقی، اصول موضوعه جدیدی برای توسعه هندسه معرفی شدند.
دو مورد از اساسی‌ترین اصطلاحات در هندسه،
خطوط و زوایا هستند. اصل پنجم اقلیدس می‌گوید که اگر یک خط مستقیم مفروض و نقطه‌ای
که روی آن خط نیست را داشته باشیم، همه خطوطی که از این نقطه عبور می‌کنند، به جز
یکی، حتماً خط مفروض را قطع می‌کنند. به عبارت دیگر، خطوط معمولی همدیگر را قطع می‌کنند،
و خطوط موازی غیرمتقاطع، چیزی غیرعادی هستند.
مفهوم زاویه به عنوان ابزاری برای توصیف
نحوه تلاقی خطوط ایجاد شد. فرض کنید مطابق شکل زیر دو خط در نقطه P یکدیگر
را قطع کنند. در این حالت دایره‌ای به مرکز P توسط خطوط به چهار قسمت تقسیم
می‌شود. اگر این قسمتها مساحت مساوی داشته باشند، این خطوط عمود برهم‌اند، و زاویه‌ها
قائم‌الزاویه هستند. این به اصل چهارم اقلیدس مربوط می‌شود.
در موارد کلی تر، زاویا بر حسب درجه
اندازه گیری می‌شوند. زوایا همچنین از طریق توابع مثلثاتی (به اینجا نگاه کنید) در حوزه‌هایی که ظاهراً
ارتباطی با هندسه ندارند نقش اساسی بازی می‌کنند.
...........................................
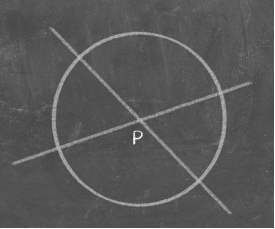
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه این کتاب می‌توانید
نسخه کامل PDF آن
را تهیه کنید.
جبر مقدماتی (Elementary
Algebra) عبارت است از هنر دستکاری
عبارات ریاضی با مقادیری که توسط علائم نشان داده می‌شوند. ولی جبر مجرد (abstract algebra) نظریه ساختارهای ریاضی انتزاعی، نظیر گروه‌ها، است (به
اینجا مراجعه کنید). استفاده از علائم به جای اعداد، این امکان را فراهم
می‌کند که به شکلِ کلی‌تری کار کنیم. x قدیمی‌ترین گزینه برای
نمایش یک عددِ مجهول، یا یک عدد دلخواه است. با استفاده از این رویکرد می‌توانیم
عبارات را دستکاری کرده و روابط بین کمیت‌ها را به روش‌های مختلف و کوتاه‌تر
بازنویسی کنیم.
مثلاً فرض کنید از ما خواسته می‌شود
عددی را پیدا کنیم که وقتی 3
به آن اضافه شود، مجموعاً 26 به دست آید. البته ما احتمالاً می‌توانیم این مسئله ساده را به طور غریزی
حل کنیم، ولی ما از نظر ریاضی می‌توانیم از یک حرف برای نشان دادن مجهول خودمان
استفاده کنیم و مسئله را بصورت معادله x+3=26 بیان کنیم. در این مثال ساده،
ما می‌توانیم ببینیم که کم کردن 3
از هر دو طرف معادله باعث می‌شود به جواب برسیم: x=26-3. جبر چیزی است که همه این نوع
دستکاری‌ها را برای ما فراهم می‌کند، هرچند معمولا فرآیندهای آن کمی پیچیده‌تر
است.
معادله یک عبارت ریاضی است که بیان می‌کند
یک چیز با چیز دیگر برابر است. پس 2 + 2 = 4 یک معادله است. همچنین E=mc2، یا x+3=26 نیز معادله هستند. هر یک از
این مثال‌ها کمی با هم متفاوتند. اولی یک اتحاد است، یعنی چیزی که همیشه درست می‌باشد.
دومی رابطه‌ای است که E را بر حسب m و c تعریف می‌کند، در حالی که
سومی معادله‌ای است که فقط برای مقدار خاصی از x صادق است. در بیشتر زمینه‌های
جبری، حداقل یک سمت معادله شامل عناصر مجهول است که معمولاً با x، y یا
z نشان داده می‌شوند. برای یافتن این مجهولات، از خیلی از تکنیک‌های
جبری استفاده می‌شود که شامل دستکاری و حل معادلات هستند.
بیشتر حوزه‌های سنجش‌پذیر، مانند علوم
خالص، اقتصاد، روانشناسی، و جامعه‌شناسی، وضعیت‌های جهان-واقعی را بر اساس معادلات
توصیف می‌کنند. به عنوان مثال، قوانین حرکتِ نیوتن در فیزیک، که برهمکنش جرم‌ها و
نیروها را توصیف می‌کنند، می‌توانند به صورت معادلاتی شامل مشتقات (به اینجا مرجعه کنید) و همچنین اعداد نوشته شوند، و
در برخی مدل‌های اقتصادی، معادلاتی هستند که قیمت کالاها را به عرضه و تقاضا پیوند
می‌دهند.
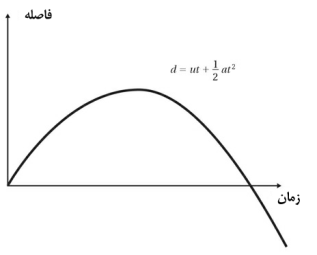
در معادله 
که در فیزیک بسیار معروف است، d نشان دهنده مسافتی است که یک
جسم با سرعت اولیه u که تحت شتاب ثابت a قرار می گیرد، طی می‌کند. در
این نمودار، فاصله بر حسب زمان رسم شده و شتاب منفی است، که در نتیجه یک منحنی به
شکل سهمی خواهیم داشت. نمونه‌ای از این شامل پرتابه‌ای است که در مقابل گرانش به
سمت بالا شلیک می‌شود.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
توابع نشان دهنده ربطه میان متغیرهای
ریاضی هستند. آنها یک ورودی را گرفته، آن را به نوعی دستکاری می‌کنند، و نهایتاً
یک خروجی تولید می‌کنند. برای مثال، تابع ƒ(x)=x+2 عددی مانند x را
گرفته و خروجی ƒ(x) را تولید می‌کند که به میزان 2
از عدد x بیشتر است. نمونه‌های پیچیده‌تر توابع شامل توابع
مثلثاتی، چندجمله‌ای‌ها، و سری‌های توانی هستند، اما انجام هر کار ریاضی بدون در
نظرگرفتن برخی از روابط تابعی که میان متغیرها وجود دارند دشوار است.
لازم نیست یک تابع برای همه مقادیر x
تعریف شود. ممکن است تابع فقط برای برخی از مقادیر، که دامنه تابع (domain) نامیده می‌شود، تعریف شود. مجموعه خروجی‌های ممکنِ یک تابع، بُرد تابع
(range) نامیده می‌شود. مجموعه‌ای از خروجی‌های واقعی تولید شده توسط یک تابع که
روی زیر مجموعه‌ای از دامنه آن اعمال می‌شود، تصویر (image) تابع است.
علیرغم اهمیت توابع، تعداد بسیار کمی
از توابع را می‌توان به راحتی تعریف و از آنها استفاده کرد. اکثر توابع توسط توابع
ابتدایی نشان داده می‌شوند یا با استفاده از آنها تقریب زده می‌شوند.
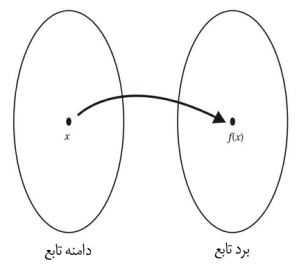
یک تابع کلیه ورودی‌هایی مانند x که در فضای معتبری به نام دامنه
تابع قرار دارند را گرفته و آنها را به فضای دیگری به نام برد تابع ƒ(x) می‌نگارد.
همراه با تابع همانی f(x)=x ،
احتمالاً تابع نمایی (exponential function) مهمترین تابع در ریاضیات است. این تابع بصورت exp(x) نوشته می‌شود و مقدار آن همیشه مثبت است، و زمانی که x به
سمت منهای بی‌نهایت میل می‌کند، این تابع به صفر میل می‌کند، و وقتی x به
بی‌نهایت میل می‌کند، مقدار آن بی‌نهایت می‌شود. با بزرگتر شدن x،
نمودار y=exp(x) نننیز تندتر می‌شود و شیب
نمودار با مقدار برابر تابع است، یعنی ارتفاع روی محور y-ها.
رفتار
خیلی از پدیده‌های متنوع، مانند فروپاشی رادیواکتیو، اپیدمی‌ها، و بهره مرکب، همگی
توسط تابع نمایی توصیف می‌شوند، و این تابع یک بلوک سازنده برای بسیاری از توابع
دیگر است. گاهی اوقات exp(x) را به صورت ex نیز می‌نویسند، که در آن e ثابت اویلر است که به
توان x
رسیده (به اینجا مراجعه کنید). همچنین
می‌توان آن را به عنوان یک سری توانی هم تعریف کرد:
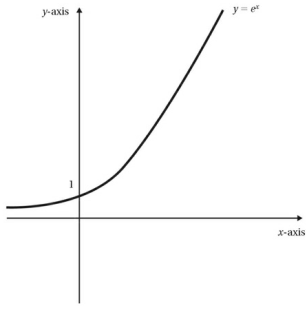
نمودار تابع نمایی با یک شیب کم شروع شده، اما با افزایش مقدار x به
سرعت تندتر می‌شود.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
از بردارها (vectors) برای نمایش کمیت‌های ریاضی یا فیزیکی که دارای اندازه یا طول، و همچنین
جهت هستند استفاده می‌شود. مثلاً باد هم سرعت و هم جهت معینی دارد. مانند آنچه در
نقشه‌های آب و هوایی نشان داده می‌شود، بردارهای آب و هوا اغلب با یک فلش نشان داده
می‌شوند که نوک پیکان و راستای پیکان جهت بردار را مشخص می‌کند، و طول آن نشان
دهنده اندازه بردار است.
هنگامی‌که نحوه ترکیب بردارها و معنای
شهودی آنها را درک کردید، خیلی از محاسبات هندسی که بدون استفاده از بردارها بسیار
پیچیده هستند، آسان می‌شوند. بنابراین بردارها مجموعه دیگری از تکنیک‌ها را برای
حل مسائل هندسی ارائه می‌کنند. داشتن راه‌های متفاوت برای نزدیک شدن به مسائل
ریاضی یکسان می‌تواند به بینش‌های جدیدی منجر شود. از آنجایی که ساختار جبری
بردارها شباهت زیادی با اشیاء ریاضی دیگر دارد، آنها بسیار مفید هستند. مجموعه‌ای
از بردارها، که به عنوان فضاهای برداری (vector spaces) شناخته می‌شوند، را می‌توان در بسیاری از زمینه‌های ریاضیات به کار برد و
کاربردهای گسترده‌ای در علوم و مهندسی دارند.
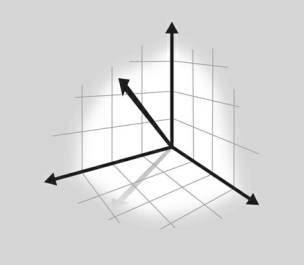
جمع دو بردار به سادگی با قرار دادن نوک
یکی از آنها به دُم دیگری، و کشیدن یک پیکان جدید از نقطه دُم اولی تا نوک دومی
بدست می‌آید. این بردار جدید به عنوان برآیند (resultant)
این دو بردار شناخته می‌شود.
بردارها را می‌توان با مختصات دکارتی
نیز توصیف کرد، که در آن نقطه (x, y) مکان نقطه پایانی (نوک
بردار) را نسبت به یک مبدا دلخواه نشان می‌دهد. درست مانند دنبال کردن نقشه گنج،
اگر x
پله در جهت xها و
سپس y
پله در جهت yها
حرکت کنیم، به هدف خود خواهیم رسید. مجموع دو بردار (1، 0) و (0، 1) را می‌توان با
جمع هر یک از مختصات آنها محاسبه کرد، که با اینکار برآیند این دو بردار (1، 1)
خواهد بود. تفریق نیز به همین صورت عمل می‌کند: حاصل (3، 2) منهای (1، 1) برابر
(2، 1) است.
از آنجا که هر یک از مختصات یک بردار یک
ضلع از مثلث قائم الزاویه را نشان می‌دهد، اندازه یا مدول (modulus) آن را می‌توان توسط قضیه فیثاغورث به دست آورد (به
اینجا مراجعه کنید). مدولِ بردارِ (1، 1) برابر است با وتر یک مثلث با
اضلاعی به طول 1، که طبق قضیه فیثاغورث، این طول با 
یا 
برابر است.
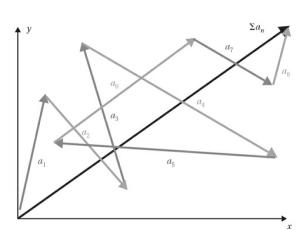
هر مسیری که توسط مجموعه‌ای از بردارها طی شود را می‌توان به یک بردار کلی
با یک جهت و بزرگی مشخص، که با حرف یونانی سیگما (∑) نشان داده می‌شود، ساده کرد.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
جبر مجرد
یا جبر انتزاعی (abstract algebra)
مطالعه ساختارهایی است که برای ترکیب عناصر یک مجموعه، از قوانین مختلفی استفاده
می‌کند. این قوانین جنبه‌های مختلف عملیاتِ جمع و ضربِ اعداد معمولی را تقلید می‌کنند
و ساختارهای ایجاد شده شامل گروه‌ها، میدان‌ها، حلقه‌ها، و فضاهای برداری هستند.
به عنوان مثال، یک فضای برداری (vector space) یک ساختار انتزاعی (مجرد) است که شامل مجموعه‌ای از
بردارها، به اضافه قوانین مربوط به آنها است. این قوانین چگونگی رفتارِ ترکیبی از
اشیاء در ساختار را توصیف می‌کنند و می‌توانند به عنوان فهرست کوتاهی از ویژگی‌ها
در نظر گرفته شوند. در فضاهای برداری، این قوانین جمعِ برداری (به اینجا مراجعه کنید) و ضربِ اسکالر (به اینجا مراجعه کنید) را توصیف می‌کنند.
این دور شدن از کاربردهای ملموسِ فضای
واقعی، و رفتن به سمت ویژگیهای انتزاعی‌تر، یک روش معمولی است که ریاضیدانان ایده‌های
خودشان را توسعه می‌دهند. علیرغم انتزاع (تجرید) و محدودیت این
ساختارهای شگفت انگیز، آنها پیامدهای گسترده‌ای در زمینه‌های مختلف، از ساختارهای
مولکولی گرفته تا توپولوژی، دارند.
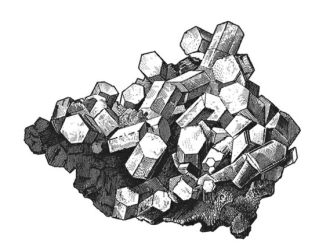
نظریه گروه‌ها نقش مهمی در درک ساختار بلورها ایفا می کند، زیرا از گروه‌های
تقارن می‌توان برای مدل‌سازی رفتار و آرایش احتمالی اتم‌ها در یک شبکه بلوری
استفاده کرد.
یک گروه (group) مجموعه ای از اعضاء، همراه با یک عملیات دوتایی است که می‌تواند به عنوان
ضرب یا جمع در نظر گرفته شود، اما در تعریف کلی گروه نامی از این عمل برده نشده
است.
برای هر مجموعه‌ای مانند G،
عمل ∙ ، و سه عضو a، b، و c، چهار ویژگی یا اصل موضوعه
عمده باید برآورده شود:
1.
بسته بودن (Closure):
یعنی اگر a و b در G باشند، پس b∙a نیز در G قرار دارد.
2.
شرکت پذيری (Associativity):
یعنی c)∙(b∙c= a∙b)∙(a.
3.
داشتن عضو
همانی (Identity): عضوی مانند e در
G وجود دارد طوری که برای همه اعضایی مانند a که
در G
قرار دارند دارد: e.a=a.
4. داشتن عضو وارون (Inverse): برای کلیه اعضایی مانند a که در G
قرار دارند، عضوی مانند a-1 در G وجود داشته باشد طوری که
a.a-1=e. عضو a-1
بعنوان عضو وارون شناخته می‌شود.
به عنوان مثال، مجموعه اعداد صحیح و عمل
جمع، یک گروه را تشکیل می‌دهند که عضو
همانی آن e=0 است، زیرا 0 تنها عددی است که می‌تواند با یک عضو جمع شود و
حاصل آن بدون تغییر بماند. همچنین از گروه‌ها می‌توان برای نشان دادن ویژگیهای
فیزیکی، مانند تقارنِ چندضلعی‌های منظم، ساختار بلورها، یا ساختار دانه‌های برف
استفاده کرد.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه این کتاب می‌توانید
نسخه کامل PDF آن
را تهیه کنید.
اعداد مختلط (Complex
numbers) تعمیمی از اعداد حقیقی هستند
که امکان وجود ریشه دوم برای اعداد منفی را فراهم می‌کنند. هر عدد مختلط مثل z را
می‌توان به صورت z=a+ib نوشت، که در آن a و b اعداد
حقیقی، و i جذر −1 است،
بنابراین i2=−1 . در اینجا a قسمت حقیقیِ z و b
قسمت موهومی آن است.
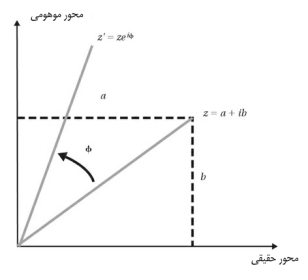
اگر (a, b) را بعنوان مختصات دکارتی یک
نقطه در نظر بگیریم، می‌توانیم هندسه اعداد مختلط را مانند شکل زیر بررسی کنیم. به
این شکل نمودار آرگاند (Argand) می‌گویند. بنابراین هر عدد
مختلطی مانند z به عنوان نقطه‌ای در صفحه، فاصله معینی از مبدأ
دارد که مدول z نامیده می‌شود و آن را بصورت |z|
نمایش می‌دهند. به راحتی می‌توان توسط قضیه فیثاغورث |z| را از دو جزء حقیقی و موهومی آن، با استفاده از
رابطه |z|2=a2+b2 حساب کرد.
هر عدد مختلط نسبت به محور x نیز
یک زاویه دارد که آرگومان (argument) z نامیده می‌شود. بنابراین یک
عدد مختلط را می‌توان بر حسب مدول آن، یعنی |z|، و آرگومان آن، یعنی θ، به
صورت z=|z|(cos θ+isin θ) مشخص کرد.
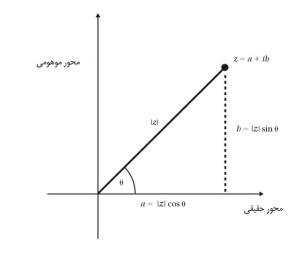
نمودار آرگاند برای یک عدد مختلط
تفسیر هندسی اعداد مختلط توسط نمودار
آرگاند، تفسیر ساده‌ای از دو ویژگی دیگر این اعداد ارائه می‌دهد. یکی از این دو
ویژگی مزدوج مختلط (complex conjugate)،
و دیگری نامساوی مثلثی (Triangle inequality) است.
مزدوجِ مختلط عددی به شکل z=a+ib،
که آن را به z* یا 
نشان می‌دهند، a-ib
است، که می‌توان آن را بعنوان تصویر نقطه z در نظر گرفت که در محور حقیقی
(x) منعکس شده است. یک محاسبه ساده نشان می‌دهد که |z|2=zz* و همچنین می‌توان قسمت‌های حقیقی
و موهومی z را برحسب مجموع و تفاضل خود عدد، و مزدوج مختلط آن
عدد، به صورت 
و 
نوشت.
نامساوی مثلثی فرمول‌بندی ریاضی این
عبارت است که می‌گوید ”ضلع بلند یک مثلث باید کوتاه‌تر از مجموع دو ضلع دیگر آن
باشد“. از نظر هندسی، مجموع دو عدد مختلط با مجموع دو بردار یکسان است (به اینجا مراجعه کنید). اجزای یک عدد مختلط
عبارتند از اجزای حقیقی و موهومی آن دو
بردار. بنابراین، اگر z، w دو عدد مختلط باشند، |z+w|≤|z|+|w|، که همان نامساوی مثلثی است.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
ترکیبات (combinatorics) شاخه‌ای از ریاضیات است که با شمارش سروکار دارد. مانند یک بازیکن پوکر
که از نظر ذهنی امکان داشتن برخی از کارت‌ها را برای بازیکنان دیگر در نظر می‌گیرد،
ترکیبات نیز به یافتن تعداد اشیاء، یا احتمالات یک رویداد، بدون نیاز به فهرست
کردن تمام نتایج مختلف مربوط است.
ترکیبات در مرکز بسیاری از مسائلِ
احتمالات، بهینه سازی، و نظریه اعداد قرار دارد. این چیزی شبیه یک هنر است، و
مبلغان معروف آن عبارتند از: لئونارد اویلر، کارل گاوس، و در تاریخ
معاصر، ریاضیدان مشهور و عجیب‌الخُلق مجارستانی، پل اردوش (Paul Erdös).
ترکیبات در گذشته به عنوان رشته‌ای
توصیف شده بود که هیچ نظریه‌ای پشت آن نیست، که حاکی از این بود که فقدان تکنیک‌ها
و روش‌های متحد کننده است. ولی این نظر در حال تغییر است و پیشرفت‌ها و موفقیت‌های
اخیری که در علم ترکیبات حاصل شده نشان می‌دهد که این حوزه در حال رشد است.
اصل لانه کبوتری (pigeonhole
principle) ایده ساده‌ای است که
کاربردهای فراوانی دارد. فرض کنید 101 کبوتر دارید. اگر فقط 100 لانه کبوتر داشته
باشید که بتوانید کبوترها را در آن نگهداری کنید، بدیهی است که حداقل یکی از 100
لانه شما باید حاوی دو یا چند کبوتر باشد. به طور کلی تر، می‌توان گفت که اگر n
جعبه و m شئ داشته باشید که m>n
، آنگاه حداقل یکی از جعبه‌ها حاوی بیش از یک شئ است.
این اصل را می‌توان در طیف گسترده‌ای از
موقعیت‌ها بکار گرفت. به عنوان مثال، می‌توان از آن برای اثبات این موضوع استفاده
کرد که در میان تمام شهرهایی که بیش از یک میلیون نفر سکنه داشته باشند،و ساکنان
آن غیر طاس باشند، حداقل دو سکنه وجود دارد که تعداد موی سرشان یکسان باشد. اثبات
آن بر این واقعیت استوار است که انسان‌ها حدود 150000 تار مو دارند، بنابراین
صرفاً برای پرهیز از خطا، حداکثر تعداد مو را 900000 فرض می‌کنیم. پس ما یک میلیون
ساکن غیر طاس (m شئ)، و 900000 موی ممکن (n جعبه) داریم. از آنجایی که m>n، اصل لانه‌کبوتری به ما می‌گوید که حداقل باید دو
شهروند وجود داشته باشند که تعداد موهایشان یکسان است.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
فضاهای متریک (metric
spaces) از مفهوم فاصله انتزاعی میان
اشیاء استفاده می‌کنند. آنها مجموعه‌هایی هستند (به
اینجا مراجعه کنید) که فاصله، یا متریک، میان عناصر در آنها تعریف
شده است. آشناترین مثال از این دست، متریک اقلیدسیِ فضای سه بعدی است که در
آن فاصله بین هر دو نقطه x و y با طول خط مستقیمی‌که آنها را
به هم وصل می‌کند به دست می‌آید.
به طور کلی تر، گفته می‌شود درصورتی یک
متریک مانند d، و یک مجموعه X، فضای متریک را تشکیل می‌دهند که d یک
تابع حقیقی از جفت نقاط در مجموعه d(x, y) باشد، و سه شرط زیر را برآورده کند:
1.
فاصله بین دو نقطه غیر منفی باشد، و اگر و فقط
اگر نقاط یکسان باشند، فاصله میان آنها صفر است.
2.
فاصله بین x و y
برابر است با فاصله بین y و x.
3. برای هر نقطه‌ای مانند z،
فاصله x تا y کمتر یا مساوی با فاصله بین x و z به
اضافه فاصله بین z و y است.
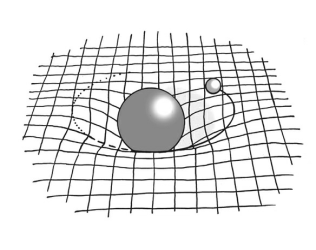
ژئودزیک (Geodesics) کوتاه‌ترین مسیر میان دو نقطه روی یک سطح منحنی است. به طور شهودی در یک
سطح صاف ما می‌دانیم که این فاصله یک خط
مستقیم است. با این حال، وقتی یک سطح انحنا دارد، ممکن است کوتاه‌ترین مسیر با یک
منحنی کلی‌تر نشان داده شود، که فاصله تعیین‌شده روی سطح را با یک متریک به حداقل
می‌رساند (اینجا را ببینید). معروف‌ترین
ژئودزیک‌های غیر-اقلیدسی دایره‌های عظیمه هستند، مانند خط استوا و مسیر
پرواز هواپیماهای دوربرد.
در بسیاری از موارد با استفاده از
انتگرال‌گیری، ژئودزیک‌ها را می‌توان به عنوان حداقل تابع دیفرانسیل که مسیرهای
بین دو جسم را توصیف می‌کند، تعیین کرد. در نظریه نسبیت عام اینشتین، ژئودزیک همین
طور توصیف می‌شود، و آنها مسیر اجسام در فضا-زمان منحنی را نشان می‌دهند. این
واقعیت که کوتاه‌ترین فاصله فضا در واقع منحنی‌های ژئودزیکی هستند، می‌تواند بی‌نظمی
مدار سیارات به دور خورشید، و انحراف نورِ اجرام نزدیک به سیاه‌چاله‌ها را توضیح
دهد.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه این کتاب می‌توانید
نسخه کامل PDF آن
را تهیه کنید.
شرلوک هلمز[1]
استدلال می‌کند ”زمانی که همه غیرممکن‌ها را حذف کردید، هر آنچه که باقی بماند، هر
چه قدر هم غیرمحتمل باشد، پاسخ شما خواهد بود.“ گفته هولمز، روش ریاضیدان است و ما از کلماتی
مانند دقت و صراحت برای توصیفِ وضعیتی که استنتاجات را ممکن می‌کند استفاده می‌کنیم
- یعنی توانایی مشاهده اینکه همه احتمالات پوشش داده شده‌اند و هیچ ابهامی وجود
ندارد و هیچ مورد خاصی وجود ندارد که به آن رسیدگی نشده باشد.
در این کتاب از کلماتِ ربطِ منطقی،
مانند ’این دلالت می‌کند‘ یا ’وجود دارد‘ یا ’برای همه‘، بدون اینکه توضیح زیادی
درباره آنها داده شود، استفاده شده، اما شایان ذکر است که خودِ منطق حوزه‌ای از
ریاضیات است.
استدلال‌های ریاضی از قواعد منطقی
استفاده می‌کنند که تعیین می‌کند چگونه می‌توان عبارات مربوط به ویژگیهای اشیاء
ریاضی را دستکاری کرد، طوری که اگر برخی از گزاره‌های ابتدایی درست باشند، گزاره‌های
ساخته‌شده از آنها نیز درست باشند. اما این فقط دستکاری نیست که معنا را ارائه می‌کند:
ویژگی‌ها و اشیائی که اینقدر انتزاعی هستند، نیاز به تعریف صوری دارند. تنها وقتی
دقیق بودن استنتاجات ما معنا پیدا می‌کند که اشیاء و ویژگیهای آنها به طور دقیق
توصیف شوند.
در حالت ایده‌آل، ریاضیات با مجموعه‌ای
از اشیاء (ابتدایی) و اصول‌موضوعه، و ویژگیهای این موارد ابتدایی شروع می‌شود.
سپس با استفاده از منطق، عبارات پیچیده‌تری از آنها ساخته می‌شود. نمونه‌هایی از
این سیستم‌های اصل‌موضوعی شامل هندسه کلاسیک (به
اینجا مراجعه کنید) و نظریه مجموعه‌ها (به
اینجا مراجعه کنید) هستند.
ما بر اساس تعاریف و شهود خودمان، یک
سری از حدس‌ها (conjecture)
را مطرح می‌کنیم. اینها عباراتی هستند که ما می‌خواهیم آنها را ثابت یا رد کنیم. حدس
اثبات شده را قضیه می‌نامند و باید صحیح، دقیق و صریح باشد. قضایا می‌خواهند
در مورد اشیائی که آنها را مطالعه می‌کنیم چیز جدیدی به ما بگویند - چیزی که به
طور منطقی از تعاریفی که با آن شروع کردیم نتیجه‌گیری می‌شود. گفته می‌شود که
ریاضیدان مجارستانی، پل اردوش (Paul Erdõs )،
زمانی گفته بود ریاضیدانان وسیله‌ای برای تبدیل قهوه به قضایا هستند[2].
نکته شگفت‌انگیز در مورد ریاضیات این
است که به نظر می‌رسد بتوان نتایجی را تولید کرد که به‌طور فوق‌العاده‌ای غیربدیهی
هستند، حتی اگر در تعریف دقیق کلمه، تکراری و زائد باشند. هرچند قضایا به طور
منطقی از حقایق فرضی پیروی می‌کنند، اما آنها بدون تلاش فراوان، آشکار نمی‌شوند.
یک اثبات (Proof) استدلالی است که یک نتیجه را نه فقط فراتر از شکِ معقول، بلکه
فراتر از هر شک دیگری تایید می‌کند. این حداقلِ اصل است. با این حال در عمل، نه وقت،
و نه جای کافی وجود دارد که بتوان هر استدلال را به دنباله کاملی از مراحل منطقی
آن تقلیل داد. بنابراین ممکن است جزئیاتی که واضح یا بدیهی بنظر می‌رسند حذف شوند،
که این می‌تواند به اشتباهاتی منجر شود که بعداً اثبات را بی‌اعتبار کند.
به سختی می‌توان به طور دقیق مشخص کرد
که چه چیزی یک اثبات را تشکیل می‌دهد. برای برخی، این یک ساختار جامعه‌شناختی است،
یعنی چیزی که ریاضیدانان بر آن توافق دارند و نقش ایجاد اطمینان را ایفا می‌کند.
برای دیگران، این دستورالعملی است که توسط یک ماشین، یا یک موجود فرازمینی که می‌تواند
نحوِ منطق را درک کند، بررسی شود.
برای فرمول بندی اثبات‌ها چندین
استراتژی مجزا وجود دارد، که کم و بیش می‌توانند برای هر مسئله‌ای موفق باشند. یکی
از هنرهای ریاضی یافتن ساده‌ترین یا زیباترین راه برای رسیدن به نتیجه است.
کتاب معروف لوئیس کارول، آلیس در سرزمین عجایب، مملو از نمونه‌هایی
از اثبات و سفسطه‌های منطقی است، که زمانی بروز می‌کنند که روش‌های منطقی به درستی
درک نمی‌شوند.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
نظریه اعداد (number
theory) شاخه‌ای از ریاضیات است که
به مطالعه خواص اعداد می‌پردازد و اغلب بر روی اعداد طبیعی تمرکز دارد (مانند همین
فصل از کتاب). اگرچه این ممکن است زیاد جالب به نظر نرسد، یا کار با اعداد طبیعی کم‌اهمیت‌تر از کار با اعداد حقیقی
یا مختلط بنظر برسد، اما اعداد طبیعی بخش ذاتیِ تصور ما در مورد جهان را تشکیل می‌دهند.
دست آوردی که بواسطه درک اعداد طبیعی، و ویژگیهای آنها حاصل شده را نمی‌توان دست
کم گرفت، و نظریه اعداد شامل برخی از عمیق‌ترین سوالات مطرح در ریاضیات است.
از آنجا که اعداد طبیعی از بلوک‌های
سازنده‌ای بنام اعداد اول ساخته می‌شوند (به
اینجا مراجعه کنید)، بسیاری از مسائل مهم در نظریه اعداد به اعداد اول
مربوط هستند. همچنین اعداد اول برای مهمترین کاربردِ نوین آنها، یعنی رمزنگاری
(cryptography)، بسیار مهم هستند. محرمانه بودن مکاتبات ایمیلی، و تراکنش‌های بانکی ما،
توسط کلیدهایی حفظ می‌شود که بر پایه مسئله تجزیه اعداد اول قرار دارند. استفاده
از اعداد اولِ بزرگ، رمزهایی را تولید می‌کند که بکارگیری آنها آسان، ولی شکستن
آنها سخت است.
مارپیچ اولام (Ulam)
یک الگوی قابل توجه در اعداد اول است. وقتی اعداد در یک مارپیچ مستطیلی ساده قرار
می گیرند، اعداد اول تمایل مشخصی به قرار گرفتن در امتداد خطوط اریب را نشان می
دهند.
اثبات وجودِ بی‌نهایت عدد اول، ابتدا در
کتاب اصول اقلیدس آمد که بیش از 2000 سال پیش نوشته شده بود. ساده ترین
رویکرد برای اثبات این قضیه، از برهان خلف استفاده می‌کند که در آن رد یک گزاره
منجر به نتیجه‌ای بی‌معنی یا متناقض می‌شود. بنابراین، ما با فرض اینکه
دقیقاً N عدد اول وجود دارد، کارمان را
شروع می‌کنیم. ما می‌توانیم این اعداد را p1, …,
pN ، بنامیم که در آن N یک عدد طبیعی متناهی است. حالا عدد x را
در نظر بگیرید که حاصل ضرب N اعداد اول در خودشان به اضافه 1 است، یعنی
x=(p1×p2...×
pN)+1
تقسیم کردن x بر هر یک از اعداد اول p1... pN
، باقیمانده 1
را باقی می‌گذارد، بنابراین x بر هیچ یک از اعداد اول
که در لیست متناهی ما قرار دارند بخش‌پذیر
نیست. اما از آنجایی که همه اعداد غیر اول را می‌توان به صورت حاصل ضرب اعداد اول
بیان کرد (به اینجا مراجعه کنید) این نشان می‌دهد
که تنها مقسوم علیه‌های x عبارتند از 1و خود x. بنابراین x باید اول باشد. اما در این
صورت، فهرست N عدد اولِ ما کامل نبوده، و این با فرض اولیه ما در
تضاد است و نشان می‌دهد که در واقع تعداد اعداد اول بی‌نهایت است.
یک مارپیچ بزرگ اولام که موقعیت 40000 عدد را ترسیم کرده . در اینجا اعداد اول به صورت نقاط
سیاه نشان داده شده‌اند.
...........................................
محتویات کامل این کتاب در 13 فصل و 400 صفحه منتشر شده، برای ادامه مطالعه
این کتاب می‌توانید نسخه کامل PDF آن را تهیه کنید.
